典型的なヘリコプターの場合ダウンウォッシュの風速はどのくらいか？

あなたが求めているのは、誘導速度 $$v_i$$ と呼ばれるものです。これは次の式で近似的に計算できます：

$$v_i = \sqrt{\frac{F_n}{2 \rho S}}$$

ここで、$$F_n$$は機体重量、$$\rho$$は空気密度、$$S$$は円盤面積である。

以下は、軽量、中量、重量のヘリコプターと、MTOW（最大離陸重量）に対する海面でのティルトローターの値の例です：

• ロビンソンR-22（軽量ヘリコプター）：ロビンソンR-22（軽量ヘリコプター）： $$7.34 \frac{m}{s}$$
• エアバスH135（中量ヘリコプタ）：$$10.01 \frac{m}{s}$$
• レナードAW139（重量ヘリコプター）：$$13.55 \frac{m}{s}$$
• ボーイングV-22オスプレイ（ティルトローターヘリコプター）：$$20.24 \frac{m}{s}$$

P.S. 最大推力はMTOW時の推力より約20%高いと推測されるので、これらの値に$$\sqrt{1.2}=1.09$$を掛けると、最大推力時の誘導速度が得られる...

ローター周辺の気流は非常に複雑である（NASAソース）：

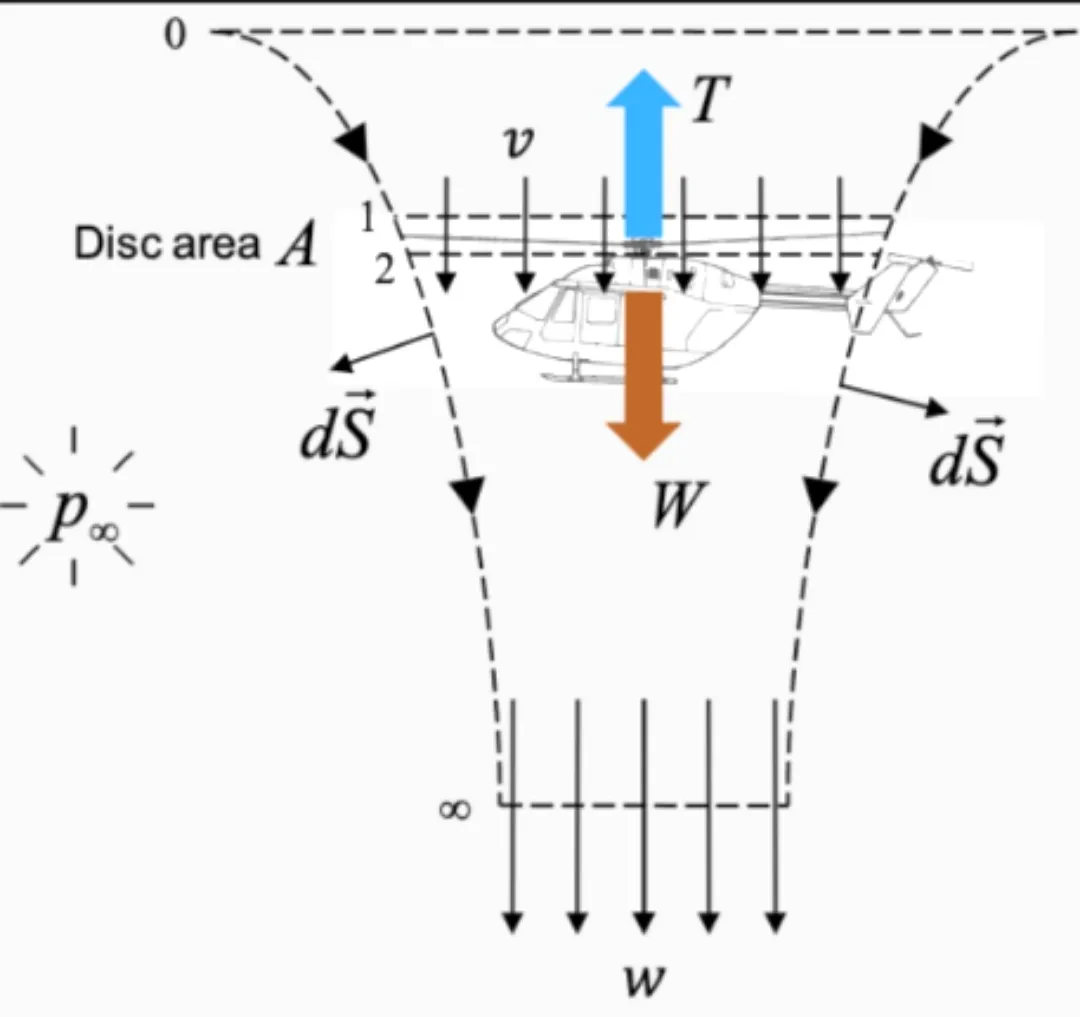
したがって、正確に一点の対気速度を推定することは非常に難しく、通常はその点がヘリコプターに属する場合にのみ行われる。いずれにせよ、平均的な流れ場の良い近似値は、ローターを薄い円盤として仮定し、その圧力で空気にジャンプを与えるという単純な運動量理論によって得ることができる（出典）：

この図に見られるように、対気速度は、ローターのはるか上方の0から、ローターのそばの$$v$$、そしてその下の$$w$$へと増加する。この特殊な対気速度の形状は「大静脈収縮」（破線）と呼ばれる。推力$T$を発生する円板面積$$A$$のローターに対して、運動量理論はローターによる速度$$v$$を次のように返す：

$$v=\sqrt{\frac{T}{2 \rho A}}$$ となる。

というように、ローターの下では気流は収縮を続け、速度は増加し、ローターの下のある直径の距離で$$w=2v$$となる。

ホバリング時の推力は重量と等しいので、この式から、質問で示された地点での速度$$w$$を計算するのは簡単である。メインローターの面積が46m²で、R22のMTOWが620kgとすると、海面では

$$w=2\sqrt{\frac{620 \times 9.81}{2 \times 1.025 \times 46}}=16m/s$$ となります。